Méthodes de clustering

Voici un post très technique pour expliciter rapidement les techniques de clustering que je mentionne de temps en temps dans d’autres billets. C’est pour le lecteur averti…

L’algorithme de Girvan et Newman

L’algorithme de Girvan et Newman est basée sur la centralité d’intermédiarité (edge-betweeness-centrality).

Cette approche est une extension des méthodes basées sur la notion de “node-betweenness centrality”. Cette notion est apparue pour la première fois dans le champ des sciences sociales pour déterminer le rôle de chaque acteur (nœud) dans un réseau social (graphe), le but étant alors de détecter des communautés partageant un intérêt commun. Cette mesure d’intérêt commun est basée sur la notion de plus court chemin dans un graphe. Si deux nœuds sont connectés, il peut exister plusieurs chemins entre eux. Les plus courts chemins sont ceux pour lesquels le nombre de nœuds sur le chemin est minimal. Il peut exister plusieurs plus courts chemins entre deux nœuds, si certains chemins ont la même longueur minimale. Intuitivement, il s’agit de repérer des « points centraux » dans le graphe autour desquels on va opérer des regroupements.

La “betweenness centrality” pour un nœud $latex k$ est alors le nombre de plus courts chemins entre deux autres nœuds $latex i$ et $latex j$ qui passent par $latex k$ (noté $latex \sigma_{ij}(k)$), divisé par le nombre total de plus courts chemins allant de $latex i$ à $latex j$ ($latex \sigma_{ij}$).

La “betweenness centrality” d’un nœud k est la somme pour toutes les différentes paires de nœuds i et j dans le graphe :

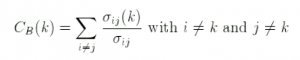
Girvan et Newman ont étendu cette notion aux arcs en définissant la “edge-betweenness centrality”. La “edge-betweenness centrality” pour un arc donné {k, k’} est la somme pour toute paire de nœud i et j (différents de k et k’) :

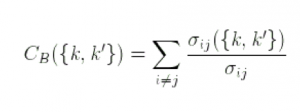
Considérons un graphe avec deux clusters de nœuds fortement interconnectés et peu d’arcs entre eux. Pour les plus courts chemins entre deux nœuds appartenant à des clusters différents, on peut voir que la plupart de ces plus courts chemins passent par les quelques arcs rejoignant les clusters ensembles. Ainsi, ces arcs ont une forte “edge-betweenness centrality”. La méthode de Girvan et Newman est basée sur cette propriété. En enlevant itérativement les arcs ayant la plus grande “edge-betweenness centrality”, les clusters du graphe sont déconnectés. La méthode de détection des clusters est un algorithme en deux passes.

• La première passe consiste à calculer la “edge-betweenness centrality” pour chaque arc du graphe, à enlever celle possédant la plus forte, puis à recalculer les “edges-betweenness centrality” pour tous les arcs du graphe résultant jusqu’à ce que tous les arcs aient été enlevés.

• La seconde passe est la construction des clusters à proprement parler. Au début, chaque cluster consiste en un unique nœud. Les arcs entre clusters sont ajoutés dans l’ordre inverse de celui dans lequel ils ont été supprimés dans la première passe. À chaque fois qu’un arc rejoint deux nœuds qui font partie de deux clusters différents, tous les nœuds des deux clusters sont groupés dans un seul cluster. À chaque fois qu’un arc joint deux nœuds qui font partie d’un même cluster, l’ensemble des clusters reste inchangé.

La méthode itérative correspondant à la seconde passe donne successivement plusieurs ensembles de clusters. En considérant l’ordre inverse de suppression des arcs, les arcs ajoutés en premier sont ceux qui ont les plus de chances d’être à l’intérieur de clusters densément connectés, et les arcs ajoutés en dernier joignent ces clusters densément connectés ensembles. Cependant, il faut déterminer quand l’algorithme change de l’un à l’autre de ces comportements extrêmes, c’est-à-dire quand la phase de construction des clusters doit s’arrêter pour maximiser la pertinence de la clusterisation. Newman et Girvan introduisent une mesure appelée “modularité” :

ou N_c est le nombre total de clusters dans un ensemble donné C, d_c est le nombre d’arcs entre les nœuds d’un cluster donné c, l_c est le degré total (c’est-à-dire le nombre total d’arcs) des nœuds dans le cluster c et L est le nombre total d’arcs dans tout le graphe. La modularité est basée sur les arcs dans le graphe original, sans tenir compte de la suppression des arcs. Cette mesure est égale à 1 si tous les arcs sont dans les clusters de C, et 0 si il y a une proportion égale entre les arcs à l’intérieur et à l’exterieur des clusters de C. L’ensemble optimal de clusters est celui dont la modularité est maximale durant la construction des clusters.

On notera que cette approche récente (2003) est considérée comme l’une des plus performantes à l’heure actuelle et réussit à partitionner des graphes ayant de l’ordre de 100000 arêtes. Ce nombre d’arêtes est par ailleurs la limite supérieure sur la taille des graphes que peuvent prendre en compte les méthodes de partitionnement non heuristiques (c’est-à-dire qui fournisse le résultat optimal).

La méthode MCL

L’algorithme MCL (Markov Cluster algorithm) est un algorithme de partitionnement rapide et capable de prendre en entrée de très grands graphes. Il est basé sur la simulation de flots stochastiques dans un graphe. Il a été mis au point par Stijn van Dongen au Centre for Mathematics and Computer Science (CWI).

Les clusters naturels dans un graphe sont caractérisés par la présence d’un grand nombre d’arcs entre les membres de ce cluster, et on peut s’attendre à ce que le nombre de chemins de longueur supérieure entre deux nœuds arbitraires dans le cluster soit grand. En particulier, ce nombre devrait être grand, relativement aux paires de nœuds appartenant à des clusters naturels différents. Vu sous un autre angle, une marche aléatoire dans le graphe va peu fréquemment aller d’un cluster naturel à un autre. L’intuition derrière l’algorithme correspond donc à ce que va faire un être humain pour repérer des regroupements de nœuds : trouver les « gros » blocs de nœuds fortement connectés, groupes qui sont eux-mêmes peu liés entre eux.

L’algorithme MCL trouve la structure en cluster d’un graphe grâce à une procédure mathématique de bootstrapping. Le processus calcule de manière déterministe les probabilités des marches aléatoires dans le graphe, et utilise deux opérateurs transformant un ensemble de probabilités dans un autre. Cela est rendu possible par l’utilisation du langage des matrices stochastiques (aussi appelées matrices de Markov), qui formalise le concept mathématique de marches aléatoires dans un graphe. Informellement, une matrice stochastique donne les probabilités de transitions entre deux nœuds d’un graphe.

L’algorithme MCL simule des marches aléatoires à l’intérieur d’un graphe en alternant deux opérations appelées expansion et inflation. L’expansion consiste à prendre la puissance d’une matrice stochastique en utilisant le produit matriciel usuel (c’est-à-dire la mise au carré d’une matrice). L’inflation consiste à prendre la puissance d’Hadamard d’une matrice, suivie d’une étape de mise à l’échelle, de telle sorte à ce que la matrice résultante soit à nouveau stochastique, c’est-à-dire que les éléments de la matrice (sur chaque colonne) correspondent à des valeurs de probabilités.

Une matrice colonne stochastique est une matrice non-négative avec la propriété que chacune de ses colonnes ait une somme égale à 1. Étant donné une telle matrice M, et un nombre réel r > 1, la matrice colonne stochastique résultant de l’inflation de chacune des colonnes de M avec le coefficient de puissance r est écrit G_r(M), et G_r est appelé l’opérateur d’inflation de coefficient de la puissance r. En écrivant S_r,j(M) pour la sommation de toutes les entrées de la colonne j de M pris à la puissance r (la somme est effectué après la mise à la puissance), G_r(M) est défini pour chaque élément par G_r(M_ij) = M_ij^r / S_r,j(M)

Chaque colonne j de la matrice stochastique M correspond à un nœud j du graphe stochastique associé à M. L’élément de la ligne i dans la colonne j (c’est-à-dire l’élément M_ij) correspond à la probabilité d’aller du nœud j au nœud i. On peut observer que pour des valeurs de r > 1, l’inflation change les probabilités associées avec la collection de marches aléatoires partant d’un nœud particulier (correspondant à la colonne d’une matrice) en favorisant les marches les plus probables par rapport aux marches moins probables.

L’expansion correspond à calculer des marches aléatoires de longueur supérieure, ce qui signifie des marches aléatoires avec beaucoup d’étapes. Il associe des nouvelles probabilités à toutes les paires de nœuds, où un nœud est le point de départ et l’autre est la destination. Puisque les chemins de longueur supérieure sont plus courants à l’intérieur d’un cluster qu’entre des clusters différents, les probabilités associées avec les paires de nœuds appartenant au même cluster vont, en général, être relativement grandes car il y a beaucoup de chemins allant d’un nœud à l’autre. L’inflation va donc avoir pour effet d’augmenter les probabilités de marches intra-cluster et va diminuer les marches inter-cluster. Ceci est obtenu sans connaissance à priori de la structure des clusters. C’est simplement le résultat de la présence d’une structure en cluster.

Finalement, itérer les expansions et inflations résulte en la séparation du graphe en plusieurs segments. Il y a plus de chemins entre ces segments, et la collection des segments résultants est simplement interprétée comme un clustering. L’opérateur d’inflation peut être altéré en utilisant le paramètre r. Augmenter ce paramètre a pour effet de rendre l’opérateur d’inflation plus fort, et cela augmente la granularité des clusters.

L’algorithme MCL peut donc s’écrire ainsi :

Fonction MCL

Paramètre : graphe M

Début

ajouter des boucles dans M

affecter à G une valeur (affecte la granularité)

affecter à M1 la matrice des marches aléatoires dans G

tant que modif

M2 = M1 * M1 (expansion)

M1 = G(M2) (inflation)

modif = difference(M1, M2)

fin tant que

Fin

Informellement, exprimé dans le langage des flux stochastiques, on peut voir que l’expansion provoque la dissipation du flux à l’intérieur des clusters alors que l’inflation élimine le flux entre les différents clusters. L’expansion et l’inflation représentent les différentes forces qui s’alternent jusqu’à ce qu’un état d’équilibre soit atteint. Un état d’équilibre prend la forme d’une matrice doublement idempotente, c’est-à-dire d’une matrice qui ne change pas avec d’autres applications des opérateurs d’expansion ou d’inflation. Le graphe associé à une telle matrice consiste en différentes composantes connexes orientées. Chaque composante est interprétée comme un cluster, et a une forme d’étoile, avec un attracteur au centre, et des arcs allant de tous les nœuds de cette composante vers l’attracteur. En théorie, des systèmes attracteurs possédant plus d’un nœud attracteur peuvent apparaitre, mais cela ne change pas l’interprétation en clusters. De plus, il peut exister des nœuds qui sont connectés à différentes étoiles, ce qui est canoniquement interprété comme des superpositions de clusters, ou en d’autres termes, certains nœuds peuvent appartenir à plusieurs clusters. Cette propriété de la méthode est d’ailleurs sans doute un avantage dans le cadre de la cartographie d’un système d’information, car on peut imaginer l’existence de nœud qui sont connecter à de nombreux clusters, mais qui ne doivent pas appartenir à un seul de ces clusters.

Pour ce qui est de la convergence, il peut être prouvé que le processus simulé par l’algorithme converge en un temps quadratique vers l’état d’équilibre. En pratique, l’algorithme commence à converger de manière visible après peu d’itérations (environ une dizaines). La convergence globale est quelque chose de très dur à prouver, mais on peut conjecturer que le processus converge toujours si le graphe d’entrée est symétrique. A noter qu’il n’y a pas de garantie mathématique à l’heure actuelle pour la convergence.

Une chose très importante à propos de l’algorithme est le fait qu’il récupère la structure en clusters via la trace laissée par cette structure sur le processus du flux. D’autres avantages de cet algorithme sont :

• il n’est pas mis en faute par des arcs liant des clusters différents,

• il est très rapide et supporte bien les fortes charges (plusieurs centaines de milliers de nœuds, la limite étant la multiplication de matrices),

• il a un paramètre naturel influençant la granularité des clusters,

• les mathématiques associées à l’algorithme montrent qu’il y a une relation intrinsèque entre le processus simulé et la structure en clusters du graphe,

• sa formulation est simple et élégante.

D’après la définition de l’algorithme MCL, on peut voir qu’il est basé sur un paradigme différent de tous les autres algorithmes basé sur des systèmes de liens. En effet, son fonctionnement est probabiliste, et sa terminaison basée sur une notion de convergence d’un processus aléatoire.

La méthode Graclus

Graclus est un logiciel qui implante l’algorithme de Dhillon, Guan et Kulis (de l’Université de Texas à Austin). L’algorithme utilise des techniques extrêmement complexes qui nécessitent un très fort background en théorie des graphes, par conséquent nous ne décrivons ici que son fonctionnement à très haut niveau. Les paramètres de l’algorithme font qu’il est difficile de l’utiliser sans fixer à l’avance le nombre de clusters que doit contenir le graphe après application de l’algorithme.

La figure suivante présente le principe à haut niveau de la méthode. L’algorithme se compose de deux phases distinctes : une phase dite de coarsening (littéralement « rendre plus brut ») du graphe, suivie d’une phase de raffinement.

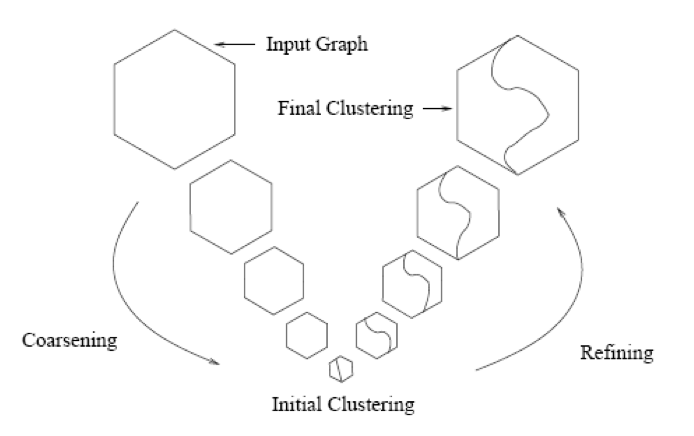
La phase de coarsening se déroule de la manière suivante : Etant donné le graphe initial G₀, on va construire des graphes de plus en plus petits G₁, G₂, … (c’est-à-dire ayant de moins en moins de nœuds). Pour passer de G_i à G_i+1, on va combiner des nœuds du premier graphe en « supernoeuds ». Le poids d’une arête (initialement 1) entre deux supernoeuds est la somme des poids des arêtes qui existaient entre les nœuds qui ont conduit aux supernoeuds considérés. L’approche de Graclus consiste, pour cette phase de coarsening, à visiter chaque sommet du graphe. Lorsqu’un sommet x n’a pas été précedemment marqué, si tous ses voisins sont marqués on le marque également, sinon on fusionne le sommet x avec un voisin non marqué y si cette fusion maximise la quantité

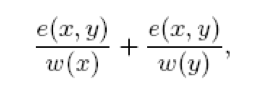
Où e(x,y) désigne le poids de l’arête entre les deux sommets et w(x) est le poids du sommet x (ce poids sur les sommets dépend des choix techniques fait sur l’algorithme, notamment en terme de ce que l’on appelle la fonction d’objectif de l’algorithme, et pas uniquement des données d’entrées de la méthode).

La phase de coarsening est itérative sur les graphes successivement crées et s’arrête lorsque l’on construit un graphe qui contient peu de nœuds. Le critère généralement retenu est la construction d’un graphe qui possède moins de 20k nœuds où k est le nombre de clusters souhaités. Arrivé à ce point, un partitionnement initial est effectué sur le dernier graphe obtenu (appelé le graphe brut) avec une méthode dite « spectrale ». C’est en raison de cette étape que la méthode est particulièrement lente (les méthodes spectrales fonctionnent en calculant les valeurs propres de la matrice qui représente le graphe, c’est-à-dire qu’elles résolvent des «équations polynomiales complexes).

Une fois cette phase finit commence une phase de raffinement dont le but est de réattribuer les nœuds fusionnés aux clusters crées lors du partitionnement initial : Si un supernoeud est dans un cluster, alors les nœuds qui ont été fusionnés pour créer ce supernoeud sont également dans le cluster.

Cet algorithme apparait réellement peu utilisable, en particulier car il faut connaitre à l’avance le nombre de clusters que doit contenir le graphe. Par ailleurs, le temps de calcul est polynomial dans le nombre de cluster, et donc la méthode n’est efficace que si le nombre de clusters est petit.