Latent Dirichlet allocation

C’est l’ami Tiger qui me l’a  demandé sur Twitter et la foule (enfin une petite foule, presque une « foulette ») en délire en a rajouté, donc voici l’article promis sur la LDA (Latent Dirichlet Allocation). Le billet va être un peu long, je vous conseille donc de vous installer confortablement. J’ai a priori gommé tous les détails techniques et j’ai essayé d’enlever tout le jargon mathématique pour juste garder l’intuition, mais il ne faut pas hésiter à me demander des précisions que j’intégrerais au texte.

Dans ce billet je vais aborder deux aspects complémentaires des techniques statistiques de modélisation des documents textuels : l’aspect génératif, et l’aspect inférence. Comme son nom l’indique le but de l’aspect génératif est de fournir une méthode de description de textes corrects, tant d’un point de vue syntaxique que d’un point de vue sémantique. Dans cette partie du billet, je me verrais obligé de présenter les méthodes plus simples de génération pour expliquer comment l’on arrive à la LDA. L’aspect inférence est lui l’aspect le plus important d’un point de vue moteur : il est celui qui permet de déterminer le sujet d’un texte par la calcul d’un score de similarité à un corpus de documents connus. Il ne faut pas croire que modèle génératif signifie méthode de génération pratique pour faire du contenu BH, loin de là !

Ce qu’il faut retenir de ce billet, c’est que récemment il y a eu une progression dans les modèles de description des documents, et que cette progression va vers des techniques qui embarquent de plus en plus de sémantique. Pour savoir ce que font les moteurs avec la LDA, direction la fin du post !

Quelques notations

Le mot sera notre unité de base, je noterai les mots par la lettre $latex w$, avec un indice pour différencier les différents mots. Un document sera donc une suite de mots que je noterai $latex d=(w_{1},\hdots,w_{n})$. Les mots sont tirés dans dictionnaire, qui contient $latex v$ mots.

Une notion importante est celle de corpus. Le corpus sera l’ensemble des mots que l’on considère, dans ce billet un corpus sera désigné par $latex C$ et sera un ensemble de documents $latex C=\{ d_{1},\hdots,d_{m}\}$.

Enfin, puisqu’il s’agit d’étudier des modélisations de documents qui embarquent de la sémantique, la notion de thématique (topic) est de la plus grande importance. Les thématiques seront toujours indiquées par la lettre $latex z$, avec des indices lorsqu’il y aura plusieurs thématiques en concurrence.

TF-IDF

Je vous ai déja parlé il y a bien longtemps de la TF-IDF dans un post, ainsi que du modèle vectoriel (et du cosinus de Salton). La TF-IDF (Term Frequency – Inverse Documents Frequency) est une mesure qui permet de faire de la ségrégation entre documents. En effet, si un terme (= mot) a une très haute fréquence dans un document, mais une fréquence basse dans les autres documents du corpus, c’est qu’il s’agit d’un terme important pour caractériser le document en question. En utilisant ensuite le modèle vectoriel, on va caractériser chaque document par un vecteur de valeurs associées à chaque mot, et c’est la comparaison entre les vecteurs qui nous donnera une mesure de la similarité entre documents.

En utilisant cette métrique pour représenter un corpus, on obtiendra une matrice de taille $latex v \times m$ qui décrit la chose suivante :

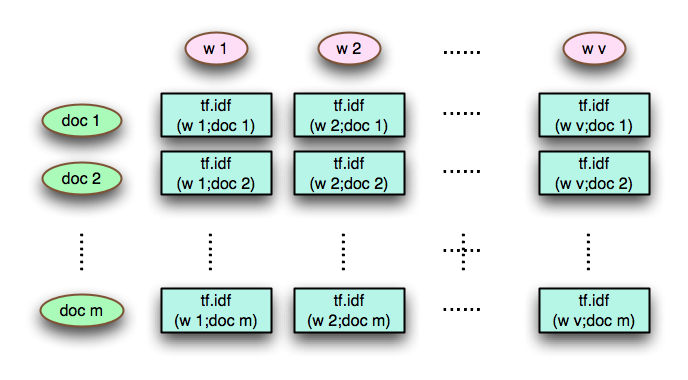
Pour vous donner une idée, le Français usuel utilise 32 000 mots, et donc si le corpus contient 1 000 000 de documents, la matrice est de taille 32 000 * 1 000 000, ce qui fait

autour de 30 GO !

Il existe des techniques de réduction de la taille de la matrice basées sur l’extraction des caractéristiques importantes, ces techniques sont basées sur la Singular Value Decomposition de la matrice. Elles sont regroupées sont le nom de LSA (Latent Semantic Analysis) dans le cas général et LSI (Latent semantic Indexing) dans le cas de la recherche d’information.

On peut tirer un modèle génératif de ce cadre de modélisation. Qu’est ce que cette bête là ? Il s’agit d’un objet qui est conçu de la façon suivante :

1. On part du principe que les données (c’est à dire les documents) obéissent à des processus aléatoires dont on ne connait pas nécessairement les paramètres.
2. On apprend les paramètres qui correspondent le mieux aux données disponibles (par exemple en calculant les fréquences)
3. On utilise le modèle avec les paramètres appris pour prédire des nouveaux documents cohérents avec ceux observés.

L’avantage des modèles génératifs est qu’ils sont particulièrement bien balisés : on sait les utiliser pour  inférer des informations sur les documents.
Bref, le modèle génératif qui se cache ici est le suivant :

En pratique un document est souvent sans thématique définie car on ne peux pas tirer au sort une thématique facilement, saud à avoir isoler à l’avance des sous-ensemble de documents qui sont dans des thématiques auparavant identifiése (à la main donc).

pLSI

le modèle pLSI (probabilistic LSI) est un modèle génératif probabiliste.
Le modèle pLSI est intéressant car c’est le premier qui introduit la notion de thématique au sein des documents. En effet, le modèle implique que la probabilité d’apparition d’un mot dans un document est fonction de la probabilité d’apparition du topic et de la probabilité d’appartenance du mot à la thématique. Si je veux écrire ça formellement, cela donne :

$latex prob(w)=\sum_{i=1}^{k} p(z_{i})p(w\mid z_{i})$ avec $latex \sum_{i=1}^{k} p(z_{i}) = 1$

Cela ne parait pas évident de prime abord, mais avec cela on a la clé pour générer des documents possédant plusieurs thématiques. Ce que j’explicite par un petit dessin :

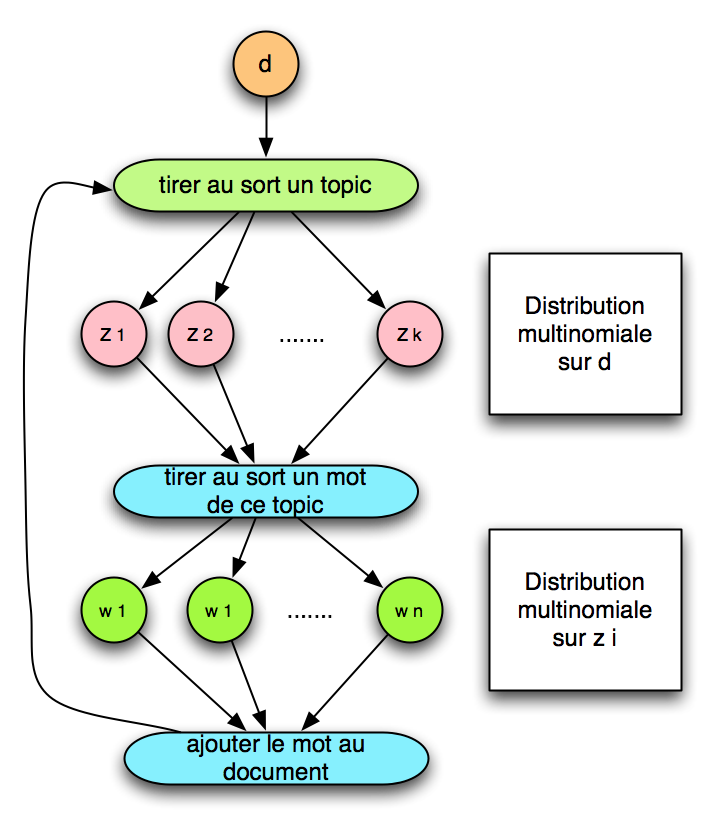
En revanche, le modèle pLSI a de multiples limitations, la première étant que les thématiques sont définies avant le document, et donc qu’un document généré a une thématique principale très marquée par les documents qui sont précédemment connus. Par ailleurs, la génération du document se fait par la probabilité d’appartenance du mot au topic, et non par la probabilité qu’un document contienne un mot d’un topic donné. Pour contrer ces limitations, on peut utiliser la LDA !

LDA

La LDA (Latent Dirichlet Allocation) est basée sur une idée beaucoup plus rusée que la pLSI. En effet, l’idée de base est qu’un document est un mélange probabiliste de thématiques latentes (c’est à dire cachées de nos yeux curieux). Ensuite, chaque thématique est caractérisée par une distribution de probabilité sur les mots qui lui sont associée. On voit donc que l’élément clé est la notion de thématique, c’est à dire que la sémantique est prioritaire sur la syntaxe (la notion de terme ou mot). C’est pour cela que l’approche est beaucoup plus puissante que les approches précédentes.

Par ailleurs, le modèle LDA a été conçu pour éviter que la distribution de probabilités qui sert au choix du topic soit dépendante des documents connus précédemment (cela signifie que le modèle est capable de prendre en compte des documents non connus à l’avance). Tout cela vient de choix techniques pas simple à comprendre. En particulier on mentionne le nom de Dirichlet car une distribution de Dirichlet permet un choix probabiliste efficace sur les distributions multinomiales (au lieu de tirer au sort un topic comme avec la pLSI, on tire d’abord au sort une méthode de tirage au sort sur les thématiques).

Au final, le procédé est le suivant :

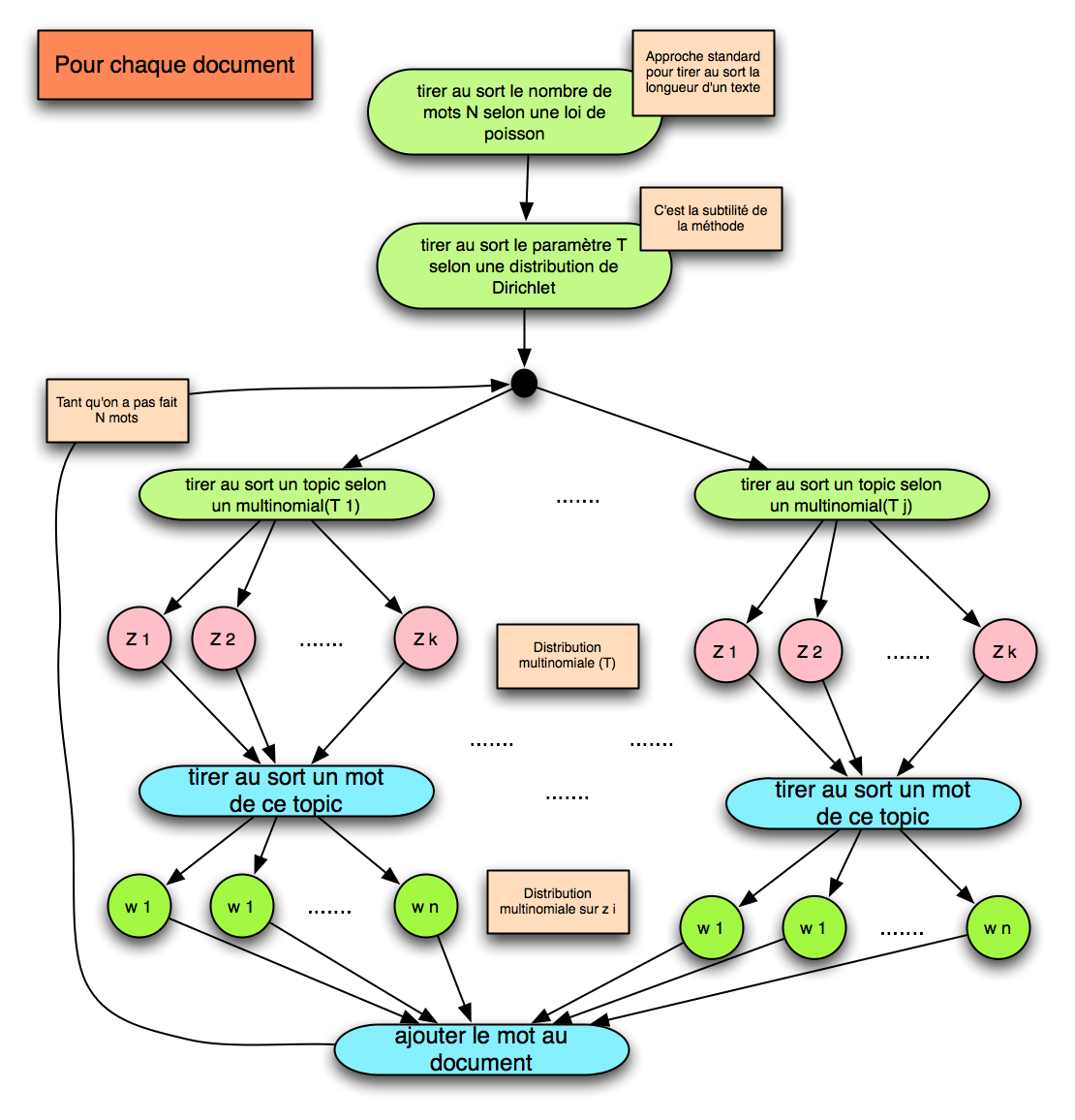
La différence avec la pLSI est donc dans l’étape sur le choix du paramètre du tirage au sort sur les topics.

L’intérêt du modèle va bien sur au delà de l’aspect génératif. Le vrai intérêt est bien sur d’inférer les thématiques à partir d’un corpus de documents. Cela se fait très bien de manière approchée, mais c’est très technique (aller donc voir ce qu’en dit Wikipedia, la partie avec les formules est celle sur l’inférence).

Inférence et LDA

Comment utiliser la LDA quand on est un moteur de recherche ? De la manière suivante :

1. Grâce à la LDA, on extrait des thématiques d’un grand corpus de documents. On va avoir quelques milliers ou plus de topics. On prend ensuite une selection de mots qui paraissent intéressants pour la ségrégation de documents (via une LSI sur le modèle TF-IDF par exemple). chaque couple (mot,topic) est caractérisé par une quantité qui est la probabilité avec laquelle un mot d’un texte est employé avec une signification qui le rattache au topic.
2. Tous ces couples sont mis dans une matrice MOT $latex \times$ TOPIC. Chaque mot est alors défini par le vecteur qui donne toutes les probas d’appartenance aux divers topics. Quand on a une requête de plusieurs mots, on peut moyenner les vecteurs pour avoir la proba d’appartenance de la requête aux topics.
3. Quand on a deux textes (ou un texte et une requête), on peut utiliser le cosinus de Salton, ou la distance de Kullback Leibler entre les vecteurs associés pour mesurer la similarité, et le tour est joué !

Il existe une utilisation exotique : le filtrage de documents (pour la lutte contre le spam) en testant un document (un mail par exemple) face à un filtre (« vous avez gagné à la loterie », « viagra gratuit », « porn 4 all », « enlarge your peniche », etc.).

Voilà, j’espère que le post vous aura plu, il y a sans doute quelques erreurs et imprécisions, je corrigerai au fur et à mesure celles que je trouve.