Annuler l’effet des structures spammantes

Aujourd’hui je vais vous parler de l’un des derniers articles acceptés que j’ai écrit avec Thomas Largillier, mon (plus pour très longtemps maintenant) thésard qui bosse sur les algorithmes pour le web. Il s’agit de l’article suivant :

Lightweight Clustering Methods for Webspam Demotion. Thomas Largillier and Sylvain Peyronnet. WI 2010.

La question que nous nous sommes posé est simple : est ce que l’on souhaite vraiment détecter le spam ? Et la réponse est non, ce que l’on souhaite c’est fournir les meilleurs résultats à l’internaute lorsqu’il requête un moteur de recherche. Et pour cela peu importe que l’index contienne 90% de bullshit si l’internaute n’est jamais emmené vers ce gros tas de spam… Bon, bien sur pour le moteur il est souhaitable de l’éliminer un minimum, mais surtout pour des raisons de coût.

Bref, ce que nous proposons c’est une approche qui a pour but d’annuler l’intérêt de la création de fermes de liens.

De l’intérêt du clustering…

Basiquement, ce que l’on va faire c’est réunir des pages qui font beaucoup trop de liens entre elles pour être honnêtes au sein d’un même cluster. Cela correspond exactement aux principes de la détection de cabale de notre algorithme SpotRank. Il existe de très nombreuses méthodes de clustering extrêmement efficaces. Par exemple le Markov Cluster Algorithm (MCL, voir [1]) et l’algorithme EBC (edge betweenness clustering, voir [2]) sont de ceux ci, mais malheureusement ils ne sont d’aucune aide pour le problème qui nous intéresse. En effet, ils ne fonctionnent pas sur des graphes aussi gros que le graphe du web. Pour MCL c’est parce que l’algorithme a besoin du graphe dans son intégralité pour faire le clustering, et pour EBC c’est parce que le temps de calcul est en $latex n^3$ avec $latex n$ le nombre de noeuds du graphe (pour nous le nombre de pages web).

Par ailleurs, trouver les clusters exacts du graphe du web est en fait le cadet de nos soucis, ce que l’on veut faire c’est regrouper des pages ensemble pour annuler l’effet d’obtention de pagerank par la création de structures « discutables », et en supprimant l’effet de 95% d’une ferme de liens, c’est un peu comme si on l’avait supprimé en intégralité.

Faute de clustering on mange des heuristiques…

Notre intérêt n’est pas, je l’ai déja dit, dans la detection mais dans l’annulation de l’effet du spam. Par ailleurs, on sait que l’algo du PageRank a une complexité en $latex O(n+m)$ avec $latex n$ le nombre de noeuds (pages web) et $latex m$ le nombre d’arêtes (liens), ainsi toute méthode de regroupement de complexité linéaire est acceptable puisque moins coûteuse que le PageRank. L’idéal (et ce que l’on propose d’ailleurs) c’est une technique que l’on peut intégrer au PageRank, et au coût quasi nul. Nous allons proposer trois méthodes de regroupements des pages entre elles, puis nous allons annuler les transferts de PageRank entre les pages d’un même regroupement (cela reviendrait en fait à fusionner toutes ces pages en une seule). Les trois méthodes sont locales, c’est à dire que pour décider si un noeud est dans un regroupement, il n’est pas utile de savoir quels sont les noeuds qui sont dans d’autres regroupements.

Méthode 1.

La première technique que nous proposons est très simple, et à l’avantage de pouvoir être intégrée au PageRank sans surcoût. Le dessin au dessous montre comment les noeuds sont regroupés pour cette technique. En rouge est le noeud d’origine du regroupement et en bleu celui qui va être regroupé avec lui. La première technique consiste donc à regrouper ensemble une page et ses pages cibles. Dans la suite je noterais cette technique Tech1.

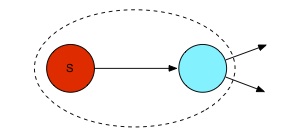
Méthode 2.

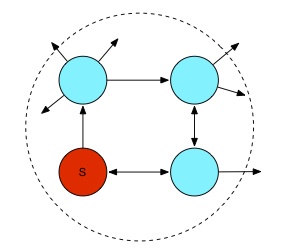
La deuxième méthode de regroupement est déjà un peu plus évoluée. Ce que l’on va faire, c’est regrouper des nœuds qui font partie de petits cycles dans le graphe. Plus précisément, on va choisir (arbitrairement) une longueur $latex k$, et à partir de chaque nœud on va calculer tous les chemins de longueur $latex k$ qui en parte. Tous les nœuds qui font partie d’un chemin qui revient à son point d’origine sont regroupés avec ce point. En pratique, nous avons choisi $latex k=3$, pour des raisons calculatoires essentiellement. L’intuition derrière ce type de regroupement est que le spammeur de base ne veut pas trop diluer son pagerank et donc qu’il va forcément générer des schémas qui reviennent vers lui.
On notera que si la longueur est 2, on shoote tous les échanges réciproques, si c’est 3 tous les échanges triangulaires, etc. Dans la suite je noterais cette technique Tech2.

Méthode 3.

La dernière méthode (Tech3) consiste à effectuer un certain nombre de marches aléatoires depuis notre page source. Ces marches sont de longueur fixée. Si le nombre de marches qui finissent sur un noeud donné dépasse un seuil fixé à l’avance, alors on va regrouper la source et le point d’arrivée. Il faut noter que l’approche est itérative (dans les 3 cas d’ailleurs) : on regroupe les noeuds en clusters, puis les clusters en clusters de clusters, etc. Ainsi deux noeuds peuvent finir dans le même cluster même si à l’origine aucune des méthodes ne les regroupaient explicitement.

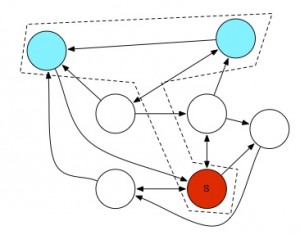
Et surprise, cela fonctionne !

La question est donc de savoir maintenant quelles sont les méthodes parmi les 3 précédentes qui sont efficaces pour casser l’effet des structures spammantes. Notre méthodologie a été de voir l’effet des regroupements sur le pagerank, puis ensuite d’utiliser un estimateur statistique pour voir si le résultat obtenu étant significatif. Nos expériences ont été effectuées sur un dataset fourni par Yahoo (voir ici). Les résultats numériques sont dans notre article, ici je ne mets que les conclusions.

Première observation : Tech1 augmente l’effet du spam, tandis que Tech2 et Tech3 diminuent son effet.

deuxième observation : Tech2 est plus efficace que Tech3 pour diminuer l’effet du spam.

troisième observation : Tech2 diminue plus que Tech3 l’importance de pages légitimes (faux positifs).

Notre dernière action a été ensuite de vérifier la validité des méthodes Tech2 et Tech3 pour séparer les pages de spam de celles légitimes (est ce que réellement les pages de spam ont un traitement différent de celles qui n’en sont pas, ou bien le comportement est-il aléatoire et donc les résultats une coïncidence). A l’aide d’un test du $latex \chi^2$, nous avons montré que Tech2 est statistiquement valide, tandis que Tech3 ne l’est pas, tech3 est donc au mieux une heuristique tandis que Tech2 est une méthode qui a un fonctionnement « prouvé » correct.

[1] Stijn Dongen. A cluster algorithm for graphs. Technical Report 10, 2000.
[2] Michelle Girvan and M. E. J. Newman. Community structure in social and biological networks. PROC.NATL.ACAD.SCI.USA, 99:7821, 2002.