About recommendation systems (3/3)

This is the last of the three posts about recommendation systems, the first can be found here, the second here.

In order to validate the effectiveness of our approach we decided to make an experiment with actual products and users. For this purpose we collected from a french medias reviews website krinein a sample of 4400 movies.  From these 4400 movies, we selected uniformly at random 160 of them. This was the data set for our experiment. We then extract uniformly at random from this data set 9 movies. These 9 movies were our witness products set.

Our methodology was then the following:

• From the people that volunteer to appear in the committee, we extract (at random) 25 of them.

• Those who did not fitted our criteria to be in the committee (same sorting of movies or the same movie appearing twice in their selection) were suppressed from the committee. We end up with 20 people in our committee. Observe that this is a number large enough for our purpose.

• It was then asked, through a web site, to the committee members to sort the 9 movies and then to choose their 5 favorite movies in the data set (these 5 movies were called the selection).

• We then asked as many people as possible to use our recommendation engine to see if it is effective. 270 people have used it so far, the experiment is ongoing so the presented results are only partial but still trustworthy. The protocol was the following, first a user is asked to sort the 9 witness movies and then we offer him two recommendations. The first one is provided by the recommendation system presented in this paper and the second recommendation is simply composed of 5 movies chosen uniformly at random in the data set.

• The users are then asked two questions for each recommendation, how many films do they like in the recommendation and how many films do they actually know in the recommendation.

The results of this experiment are presented in the following figures.

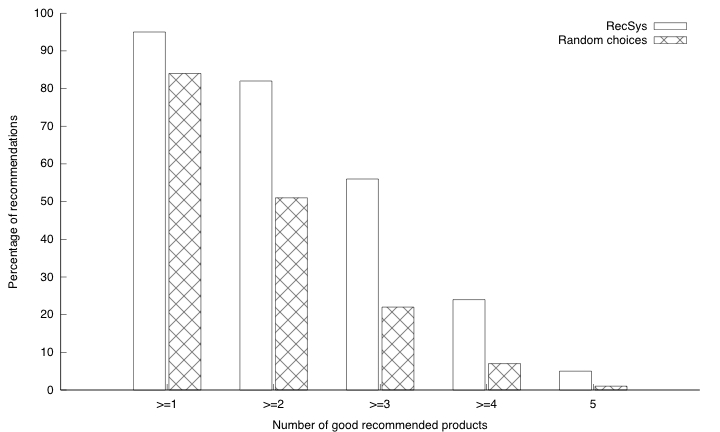
This figure shows the percentage of recommendations that contains at least a given number of good recommended products (e.g. products liked by user). It first gives the percentage of good recommendations (according to the definition I gave in a previous post). Our method clearly outperforms the random recommendation since we achieve a percentage greater than $latex 95\%$ while the random recommendation only achieves less than $latex 85\%$.  Moreover, we can see that our recommendation scheme also provides higher order good recommendations (that is recommendation of several good products). On the other hand, random choices’ effectiveness drops quickly and it often fails to provide users with more than 2 good products.

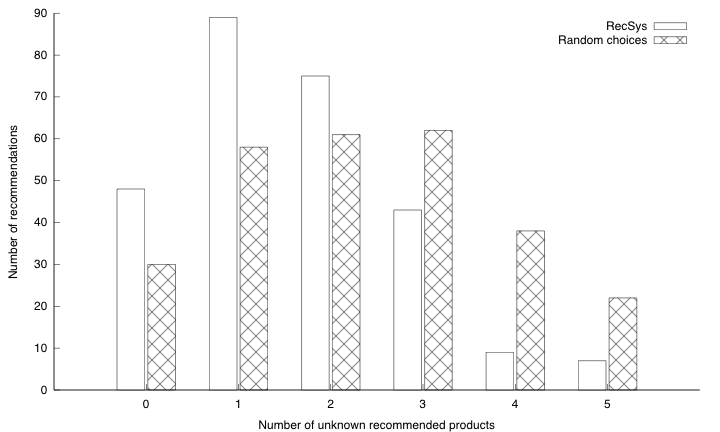
This one shows the number of recommendations w.r.t. the number of unknown products recommended.  A too large number (i.e. 4 or 5) of unknown products seems to indicate a poor quality of recommendation since we are here dealing with well known movies: if one does not know items recommended too him, it is likely that they are in fact movies he did not want to see.  It is also important to note that if this number is to high it will decrease the user’s confidence in the recommendation. We can clearly see on the figure that this number decrease much faster with our algorithm than with the random choices. On the contrary, recommending only known products is not good for the user experience, but is not a drawback for our experiment.

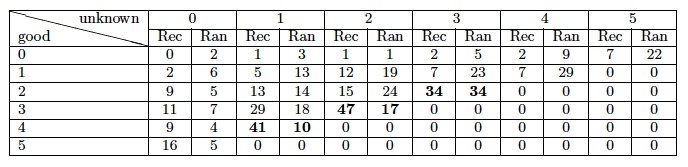
We also want to compare the « quality » of the recommendations made by both techniques. Meaning we want to compare the number of good recommended products w.r.t. the number of unknown products in the recommendation. The results are summed up in the table above. In this table, the columns are indexed by the number $latex nu$ of unknown products in the recommendations and the rows are indexed by the number $latex ng$ of good products in those recommendations. We can see in the table that when $latex (ng, nu) \in \{(2, 3), (3, 2), (4, 1)\}$ our algorithm outperforms the random choices. These cases are interesting because they concern good recommendations where $latex (ng + nu = 5) \wedge (ng > 1) \wedge (nu < 5)$, thus the user is confident in the recommendation (he liked all the movies he knows in the recommendation) and will probably consult the unknown products.

All in all, this experiment shows the effectiveness of our approach: it is possible to provide users with good recommendations with high probability (but low complexity).