About recommendation systems (2/3)

This is the second post about recommendation systems, the first one can be found here.

It is pretty obvious that the goal of a recommendation system is to provide users with « good » products. I am going to first introduce our notations and then explain what is a good recommendation in our framework. In the work done with Sebastien hemon and Thomas Largillier, we consider that users belong to a set $latex \mathcal{U} = \{ u_{1} \cdots u_{m} \}$ of $latex m$ distinct users and that products come from $latex \mathcal{P} =\{ p_{1} \cdots p_{n} \}$, a set of $latex n$ distinct products.  We also suppose that we are given, even implicitly, a function $latex f : \mathcal{U} \times \mathcal{P} \longrightarrow \mathbb{R} $ that gives for every couple of user/product a utility; $latex f$ is then a so-called utility function. We only assume that the utilities obey to the classical ordering relation induced by $latex \mathbb{R}$. This means that every user has a rational behaviour (this assumption is usual, see for instance the book A course in Game Theory by  Martin Osborne).

We then defined a recommendation system as a function $latex \mathcal{R} : \mathcal{U} \rightarrow \mathcal{P}_r$, where $latex \mathcal{P}_r = \{X \subseteq 2^{\mathcal{P}}, |X|=r \}$. It means that for each user $latex u_i$, $latex \mathcal{R}(u_i)$ is a set of $latex r$ products ($latex r$ is a somehow magically chosen parameter). If we denote by $latex \mathcal{F}_r (u_i )$ the $latex r$ favorite products (according to $latex f$) of user $latex u_i$, we can say that a good recommendation occurs when we have:

$latex \mathcal{F}_r (u_i ) \cap \mathcal{R} (u_i ) \neq \emptyset$

Of course, we aim to obtain an algorithm that gave, most of the time, a good recommendation.

We used the modelling I just defined above and designed an algorithm built on several assumptions.  First, we consider that we want our recommendation system to output a good recommendation of $latex r$ products, where $latex r$ is a very small integer (typically it will be $latex r=5$ in practical experiments that I will present in a third post).  It is often admitted that, to get a good recommendation, users follow some kind of behavior which can be viewed as arbitrary distinct classes. In our method we used the notion of product sorting equivalence and $latex r$-equivalence. I won’t go into too much technical details on these equivalence relations but basically they states that users from the same class sort the products in the same order (product sorting), and that users from the same class have the same $latex r$ favorite products ($latex r$-equivalence). Thus, we do not admit that users behave the same, exactly or modulo some randomized perturbations, but only tell that there is a model that, given a ranking of products for each user, naturally sort users into equivalence classes. All of our work was done according to two assumptions.  The first is that we consider that we can have access to a few users who will rank a set of witness products and give their $latex r$ favorite products. These users will be known as « the committee ». The second assumption is that we are authorized to ask every people about these witness products. This two hypothesis allow us to say that our recommendation system uses partial information in order to make its recommendation.

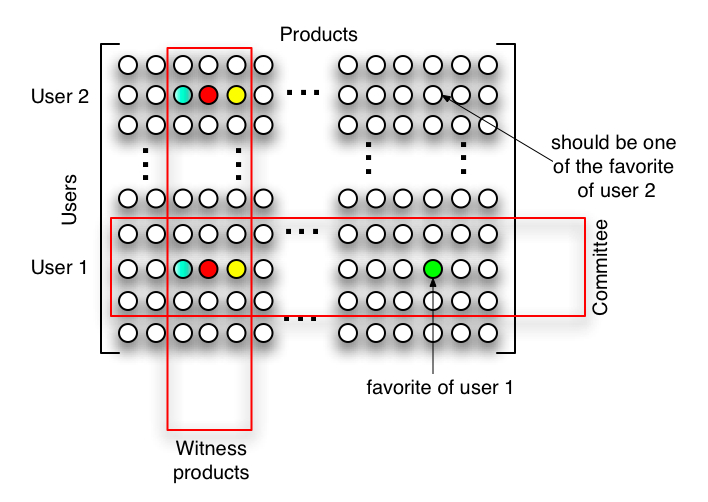
Within this framework, our algorithm is quite simple (see figure above). We first choose a committee, ask to each member of the committee to sort some products according to its preferences. Then we choose a set of witness products and ask all users to sort those products.  Once this is done, we can cluster with high confidence users into equivalence classes according to the two equivalence relations defined above. The given clustering will likely attribute at least one member of the committee to each equivalence class. This peculiar user will be use in order to make recommendations to member of its class.

The main issue to ensure a good recommendation is to understand what should be the size of the committee, and how many witness products we need.  Note that, in our algorithm, the only difference between committee member and other users is that committee users gave their favourite products in addition to the information about witness products.